Soal matematika kelas 6 semester 2. Pada postingan ini kami akan mencoba membagikan 100+ Soal Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi Terbaru. Di mana soal matematika kelas 6 ini disusun berdasarkan kisi kisi yang sedang berlaku di saat ini. Lantas seperti apa soal matematika kelas 6 semester 2 dan kunci jawabannya pdf ini?
Soal Matematika Kelas 6 Semester 2 Kurikulum 2013
Contents
Untuk soal matematika kelas 6 semester 2 2021 ini kami merangkumnya menjadi beberapa bagian. Pembagian ini berdasarkan materi atau kompetensi dasar yang ada di semester 2 ini. Adapun materi Matematika kelas 6 semester 2 ini meliputi:
- materi lingkaran,
- mengenal bangun ruang,
- menghitung volume bangun ruang,
- luas permukaan bangun ruang,
- statistika ( mencari modus, median dan mean ).
Nah dari beberapa bab di atas akan kami bahas satu per satu melalui contoh soal matematika kelas 6 dan kunci jawabannya. Mari kita simak dan pelajari bersama sama!
Soal Matematika Kelas 6 Lingkaran
Untuk membantu adik adik memahami materi materi lingkaran kelas 6 sd pdf. Berikut ini kami berikan beberapa contoh soal lingkaran beserta jawabannya. Di mana di dalamnya juga terdapat soal cerita matematika kelas 6 lingkaran. berikut ini penjelasnya selengkapnya!
1. Diketahui sebuah Iingkaran mempunyai jari – jari 50 cm. Keliling Iingkaran tersebut adalah….
a. 157 cm
b. 314 cm
c. 7.550 cm
d. 7.850 cm
Jawaban:
Keliling lingkaran = 2 x π x r
= 2 x 3,14 x 50
= 3,14 x ( 2 x 50 )
= 3,14 x 100
= 314 cm.
2. Perhatikan gambar lingkaran di bawah ini !
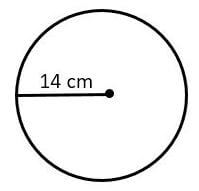
Keliling bangun tersebut adalah ….
a. 44 cm
b. 88 cm
c. 616 cm
d. 1.254 cm
Jawaban:
Keliling lingkaran = 2 x π x r
= 2 x 22/7 x 14
= 2 x 22 x 2
= 44 x 2
= 88 cm
3. Sebuah Iingkaran mempunyai luas 3.850 cm². Maka panjang jan-jan Iingkaran tersebut adalah
a. 21 cm
b. 25 cm
c. 35 cm
d. 49 cm
Jawaban:
Luas lingkaran = π x r x r
3.850 = π x r x r
3.850 = 22/7 x r²
3.850 : 22/7 = r²
r² = 3.850 : 22/7
r² = 3.850 x 7/22
r² = 175 x 7
r² = 1.225
Maka r = √1.225
= 25 cm.
4. Perhatikan gambar lingkaran berikut ini !

Luas bagian yang diarsir adalah ….
a. 966,25 cm²
b. 866,25 cm²
c. 693 cm²
d. 593 cm²
Jawaban:
Luas arsiran di atas = 5/8 x luas lingkaran
= 5/8 x π x r x r
= 5/8 x 22/7 x 21 x 21
= 5/8 x 22 x (21 : 7) x 21
= 5/8 x 22 x 3 x 21
= 5/8 x 66 x 21
= (5 x 66 x 21) : 8
= 6.930 : 8
= 866,25 cm²
5. Adib berlari mengelilingi lapangan yang berbentuk Iingkaran sebanyak 6 kali. Apabila diameter lapangan tersebut adalah 35 meter. Maka jarak yang ditempuh oleh Adib adalah … meter.
a. 100 m
b. 110 m
c. 650 m
d. 660 m
Jawaban:
Untuk menyelesaikan soal di atas adalah keliling lapangan (lingkaran) x banyaknya mengelilingi lapanagan
Maka akan sebagai berikut:
Jarak yang ditempuh = Keliling lingkaran x banyaknya berputar
= π x diameter x banyaknya berputar
= 22/7 x 35 x 6
= 22 x (35:7) x 6 bisa juga (22 x 35 x 6) : 7
= 22 x 5 x 6
= 110 x 6
= 660 m.
Soal PAS Matematika Kelas 6 Lingkaran
6. Perhatikan gambar di bawah ini!

Luas daerah yang diarsir adalah ….. cm².
Jawaban:
Diketahui :
Diameter = 28 cm maka jari jari (r) = 14 cm
Luas arsiran = ½ x luas lingkaran
= ½ x π x r x r
= ½ x 22/7 x 14 x 14
= ½ x 22 x (14 :7) x 14
= ½ x 22 x 2 x 14
= ½ x 44 x 14
= 22 x 14
= 308 cm²
7. Keliling lingkaran dengan jari-jari 10 cm adalah …..cm. (π = 3,14)
Jawaban:
Keliling lingkaran = 2 x π x r
= 2 x 3,14 x 10
= 3,14 x (2 x 10) menggunakan sifat asosiatif / pengelompokan perkalian.
= 3,14 x 20
= 62,8 cm.
Soal Ulangan Matematika Kelas 6 Lingkaran
8. Di samping sekolah terdapat sebuah taman. Taman tersebut berbentuk Iingkaran dengan diameter 28 meter. ¾ bagian dari taman ditanami rumput dan sisanya dibuat kolam. Berapa luas bagian dari taman yang dibuat kolam?
Jawaban:
Bagian yang dibuat kolam = 1 – ¾ = ¼ makayang kita lakukan mencari ¼ bagian dari taman atau ¼ bagian dari luas lingkaran.
Luas kolam = ¼ x luas lingkaran
= ¼ x π x r x r
= ¼ x 22/7 x 28 x 28
= ¼ x (28 : 7) x22 x 28
=( ¼ x 4) x 22 x 28
= 1 x 22 x 28
= 616 cm².
Soal Matematika Kelas 6 Semester 2 tentang Bangun Ruang
1. Sebuah kubus mempunyai panjang rusuknya 10 cm. Maka berapakah luas permukaan kubus tersebut?
a. 600 cm²
b. 400 cm²
o. 200 cm²
d. 100 cm²
Jawaban:
Luas permukaan kubus = 6 x r x r
= 6 x 10 x 10
= 60 x 10
= 600 cm².
2. Hani memiliki kotak berbentuk balok dengan ukuran panjang 25 cm dan lebar 10 cm. Jika volume balok tersebut 2.000 cm3 maka berapakah tinggi balok tersebut?
a. 8 cm
b. 10 cm
c. 12 cm
d. 15 cm
Jawaban:
Volume balok = p x l x t
2.000 = 25 x 10 x t
2.000 = 250 x t
(2.000 : 250) = t
Maka t = 2.000 : 250 = 8 cm.
3. Perhatikan gambar jaring jaring bangun ruang berikut ini !
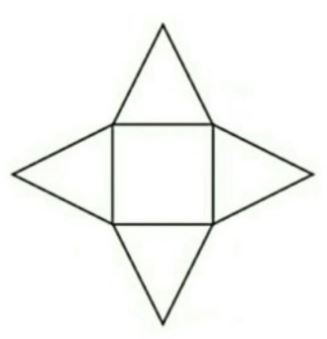
Gambar tersebut merupakan jaring-jaring dari bangun ….
a. Kerucut
b. Prisma
c. Limas
d. Kubus
Jawaban:
Jaring jaring di atas merupakan jaring jaring limas, tepatnya limas segiempat.
4. Sebuah kerucut berukuran seperti gambar berikut ini.
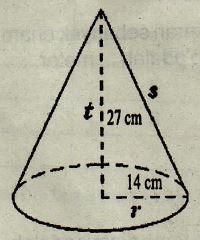
Volume kerucut tersebut … cm3.
a. 2.834 cm³
b. 2.844 cm³
c. 5.534 cm³
d. 5.544 cm³
Jawaban:
Volume kerucut = 1/3 x luas alas x tinggi
= 1/3 x luas lingkaran x tinggi
= 1/3 x π x r x r x t
= 1/3 x 22/7 x 14 x 14 x 27
= 1/3 x 22 x (14:7) x 14 x 27
= 1/3 x 22 x 2 x 14 x 27
= (1/3 x 27) x 44 x 14
= 9 x 44 x 14
= 5.544 cm³.
5. Sebuah bak penampungan air berbentuk tabung dengan panjang diameter 20 dm dan tinggi 60 dm. Jika bak tersebut berisi air dengan ketinggian 40 dm maka volume air dalam tabung tersebut adalah …. dm³.
a. 12.460
b. 12.560
c. 18.740
d. 18.840
Jawaban:
Diameter = 20 dm maka r = 10 cm.
Tinggi yang digunakan 40 dm bukan yang 60 dm.
Volume tabung = luas alas x tinggi
= luas lingkaran x tinggi
= π x r x r x t
= 3,14 x 10 x 10 x 40
= 314 x 40
= 12.560 dm3
Soal Matematika Kelas 6 Semester 2 Kurikulum 2013 Bangun Ruang
6. Sebuah tabung dengan diameter 70 cm dan tinggi 25 cm maka volumenya adalah …. cm3.
Jawaban:
Diketahui:
Diameter = 70 cm maka jari jari (r) = 35 cm
Tinggi (t) = 25 cm
Volume tabung = luas alas x tinggi
= luas lingkaran x tinggi
= π x r x r x t
= 22/7 x 35 x 35 x 25
= 22 x (35 : 7) x 35 x 25
= 22 x 5 x 35 x 25
= 110 x 875
= 96.250
7. Limas segi empat mempunyai bidang sisi sebanyak ….
Jawaban:
Limas segi empat mempunyai
– Sisi sebanyak 5 buah.
– Titik sudut sebanyak 5 buah.
– Rusuk sebanyak 8 buah.
8. Pak Edy mempunyai kaleng berbentuk kubus dengan panjang rusuk 30 cm. Apabila kaleng tersebut berisi minyak 1/5 bagian. Maka berapa cm3 volume minyak di dalam kaleng tersebut?
Jawaban:
Diketahui:
Panjang rusuk kubus (r) = 30 cm
Ditanya:
Volume 1/5 bagiannya = …. ?
Jawab:
Volume 1/5 bagiannya = 1/5 x volume kubus
= 1/5 x r x r x r
= 1/5 x 30 x 30 x 30
= (30 : 5) x 30 x 30
= 6 x 30 x 30
= 180 x 30
= 5.400 cm³.
Soal Matematika Kelas 6 Semester 2 dan Kunci Jawabannya Bangun Ruang
9. Perhatikan gambar di bawah ini
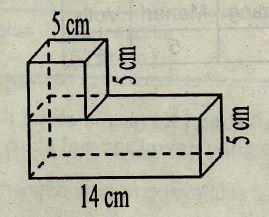
Volume bangun tersebut adalah ….
a. 475 cm³
b. 425 cm³
c. 375 cm³
d. 225 cm³
Jawaban:
Volume gabungan di atas merupakan gabungan dari bangun kubus dan balok.
Volume gabungan = V kubus + V balok
Volume kubus = r x r x r
= 5 x 5 x 5
= 125 cm³
Volume balok = p x l x t
= 14 x 5 x 5
= 70 x 5
= 350 cm³
Volume gabungan = V kubus + V balok
= 125 + 350
= 475 cm³.
10. Perhatikan gambar berikut ini !

Bangun ruang tersebut adalah gabungan dari bangun ruang … dan ….
a. balok dan kubus
b. balok dan kerucut
c. balok dan prisma
d. balok dan limas
Jawaban:
Bagian bawah merupakan bangun balok.
Bagian atas merupakan bangun prisma.
11. Perhatikan gambar bangun ruang di bawah ini!

Luas permukaan bangun tersebut adalah …. cm²
a. 128
b. 192
c. 214
d. 224
Jawaban:
Luas permukaan bangun ruang di atas = LP Balok + LP Kubus
Luas Permukaan Balok (sebelah kiri) = 2 x ((p x l) + (p x t) + (l x t))
= 2 x ( (4 x 4) + (4 x 8) + (4 x 8))
= 2 x (16 + 32 + 32)
= 2 x (48 + 32)
= 2 x 80
= 160 cm².
Luas permukaan kubus (sebelah kanan) = 6 x r x r karena yang nampak hanya 4 bagian saja maka
= 4 x 4 x 4
= 64 cm³
Luas permukaan gabungan bangun ruang di atas = LP Balok + LP Kubus
= 160 + 64
= 22 cm³
Soal Matematika Pilihan Ganda
12. Perhatikan gambar di bawah ini !
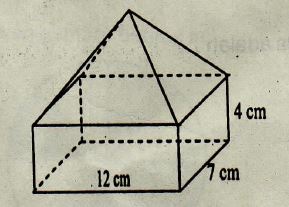
Apabila tinggi limas tersebut adalah 6 cm, maka berapakah volume bangun tersebut?
a. 504 cm³
b. 432 cm³
c. 336 cm³
d. 326 cm³
Jawaban:
Volume gabungan bangu ruang di atas = V Balok + V Limas
Volume Balok (bagian bawah) = p x l x t
= 12 x 7 x 4
= 84 x 4
= 336 cm³
Volume limas segiempat = 1/3 x luas alas x tinggi
= 1/3 x p x l x t
= 1/3 x 12 x 7 x 6
= (12 : 3) x 7 x 6
= 4 x 7 x 6
= 28 x 6
= 168 cm³
Volume gabungan bangu ruang di atas = V Balok + V Limas
= 336 + 168
= 504 cm³.
13. Perhatikan gambar di bawah ini!

Volume bangun gabungan tersebut di atas adalah ….
a. 19.404 cm³
b. 33.264 cm³
c. 42.668 cm³
d. 52.668 cm³
Jawaban:
Volume gabungan = V tabung + V ½ bola
Volume tabung (bagian bawah) = luas alas x tinggi
= π x r x r x t
= 22/7 x 21 x 21 x 24
= 22 x (21 : 7) x 21 x 24
= 22 x 3 x 21 x 24
= 66 x 504
= 33.264 cm³
Volume ½ bola (bagian atas) = ½ x 4/3 x π x r x r x r
= ½ x 4/3 x 22/7 x 21 x 21 x 21
= (4 : 2) x 22 x (21 : 3) x (21 : 7) x 21
= 2 x 22 x 7 x 3 x 21
= 44 x 21 x 21
= 44 x 441
= 19.404 cm³
Volume gabungan = V tabung + V ½ bola
= 33.264 + 19.404
= 52.668 cm³
14. Perhatikan gambar berikut ini !
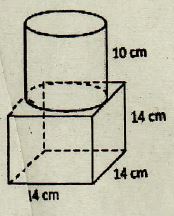
Volume bangun gabungan di atas adalah …. cm³
Jawaban:
Volume gabungan = V kubus + V tabung
Volume kubus (bawah) = r x r x r
= 14 x 14 x 14
= 196 x 14
= 2.744 cm³
Volume tabung (atas) = luas alas x tinggi
= π x r x r x t
= 22/7 x 7 x 7 x 10 ( mengapa r nya 7 karena 14 cm di gambar merupakan diameternya tabung).
= 22 x (7 : 7) x 7 x 10
= 22 x 1 x 7 x 10
= 22 x 70
= 1.540 cm³.
Volume gabungan = V kubus + V tabung
= 2.744 + 1.540
= 4.284 cm³.
15. Lihat gambar berikut !
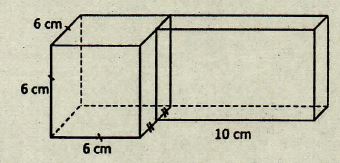
Luas permukaan bangun gabungan di atas adalah …. cm²
Jawaban:
Luas permukaan bangun gabungan = luas permukaan kubus + balok
Luas permukaan kubus = 6 x r x r ( rusuk = 6 cm)
= 6 x 6 x 6
= 216 cm².
Balok dengan ukuran:
P = 10 cm
l = 3 cm ( separuh dari panjang rusuk kubus di sampingnya)
t = 6 cm.
Luas permukaan balok = 2 x ((p x l) + (p x t) + (l x t))
= 2 x ((10 x 3) + (10 x 6) + ( 3 x 6))
= 2 x ( 30 + 60 + 18 )
= 2 x 108
= 216 cm²
Maka:
Luas permukaan bangun gabungan = luas permukaan kubus + balok
= 216 + 216
= 432 cm²
Soal Cerita Matematika Bangun Ruang Kelas 6
1. Sebuah cetakan kue berbentuk gabungan dari bangun tabung dan kerucut. Diameter tabung tersebut yaitu 42 dm dan tingginya 50 dm. Jika tinggi kerucut 18 dm, berapa liter volume cetakan kue tersebut?
Jawaban:
Volume gabungan = V tabung + v kerucut
Volume tabung = luas alas x tinggi
= luas lingkaran x tinggi
= π x r x r x t
= 22/7 x 21 x 21 x 50
= 22 x (21 : 7) x 21 x 50
= 22 x 3 x 21 x 50
= 66 x 1.050
= 69.300 dm³.
Volume kerucut = 1/3 x luas alas x tinggi
= 1/3 x luas lingkaran x tinggi
= 1/3 x π x r x r x t
= 1/3 x 22/7 x 21 x 21 x 18
= 22 x (21 : 3) x (21 : 7) x 18
= 22 x 7 x 3 x 18
= 154 x 54
= 8.316 dm³
Volume gabungan = V tabung + v kerucut
= 69.300 + 8.316
= 77.616 dm³.
Soal Matematika Kelas 6 Statistika
Perhatikan daftar kegemaran siswa kelas VI SD Pena Pengajar di bawah ini!
- Membaca : 6 anak
- Sepak Bola : 9 anak
- Berenang : 5 anak
- Menari : 5 anak
- Bola Volly : 8 anak
Modus kegemaran siswa kelas VI tersebut di atas adalah ….
a. Membaca
b. Sepak Bola
c. Berenang
d. Volly
Jawaban:
Untuk mencari modus dari daftar kegemaran di atas maka kita cari kegemaran yang banyak diminati siswa atau anak, yaitu sepak bola. Sepak bola diminati oleh 9 anak.
2. Berikut ini daftar nilai yang didapat oleh Alvino dari beberapa kali ulangan:
6, 6, 8, 8, 9, 9, 7, 7, 10, 5,
7, 6, 5, 10, 10, 10, 8, 8, 9, 10.
Median dari data tersebut yaitu ….
a.5 .
b. 7
c. 8
d. 9
Jawaban:
Untuk mencari median, terlebih dahulu kita urutkan data tersebut dari yang terkecil ke yang terbesar, sehingga:
5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10
Untuk menentukan letak median kita gunakan rumus di bawah ini:
(Jumlah data + 1) : 2 maka
= (20 + 1) : 2
= 21 : 2
= 10,5
Maka letak mediannya di antara data no. 10 dengan no. 11.
Sedangkan data:
No. 10 adalah 8.
No. 11 juga 8
Maka Median = ( 8 + 8 ) : 2
= 16 : 2
= 8.
3. Di bawah ini merupakan data berat badan siswa kelas VI SD Pena Pengajar
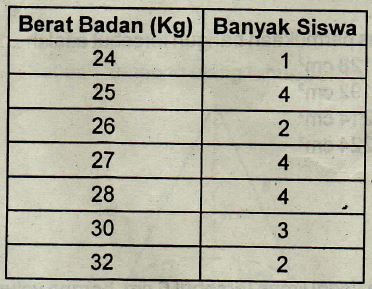
Dari data di atas maka rata-rata berat badan siswa kelas VI SD Pena Pengajar adalah ….
a. 27,5 kg
b. 27,4 kg
c. 26,7 kg
d. 26,5 kg
Jawaban:
24 x 1 = 24
25 x 4 =100
26 x 2 = 52
27 x 4 = 108
28 x 4 = 112
30 x 3 = 90
32 x 2 = 64
Jumlah nilai = 24 + 100 + 52 + 108 + 112 + 90 + 64
=124 + 160 + 202 + 64
= 284 + 266
= 550
Jumlah data = 1 + 4 + 2 + 4 + 4 + 3 + 2
= 5 + 6 + 7 + 2
= 11 + 9
= 20
Rata rata = jumlah nilai : jumlah data
= 550 : 20
= 27,50.
4. Diagram batang di bawah ini menunjukkan data penjualan beras di Toko Sami Murah.
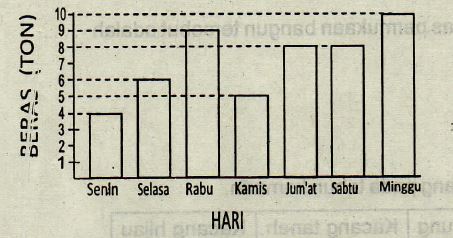
Maka Rata-rata penjualan beras di Toko Sami Murah di tiap harinya adalah ….
a. 6,01 ton
b. 7,01 ton
c. 7,14 ton
d. 8,14 ton
Jawaban:
Senin = 4 ton
Selasa = 6 ton
Rabu = 9 ton
Kamis = 5 ton
Jum’at = 8 ton
Sabtu = 8 ton
Minggu = 10 ton
Jawab:
Jumlah nilai = 4 + 6 + 9 + 5 + 8 + 8 + 10
= 10 + 14 + 16 + 10
= 24 + 26
= 50
Jumlah data = 7 ( Senin sd Minggu = 7 hari ).
Rata rata = jumlah nilai : jumlah data
= 50 : 7
= 7,14 ton
5. Hasil dari pengukuran tinggi badan pemain bola Pena FC adalah sebagai berkut.
172, 167, 180, 170, 169, 160, 170, 165, 173, 170
Modus dari tinggi badan pemain bola tersebut adalah ….
a. 167
b. 169
c. 170
d. 173
Jawaban:
167 cm ada 1 pemain.
169 cm ada 1 pemain.
170 cm ada 3 pemain.
173 cm ada 1 pemain.
Maka modusnya adalah 170 cm karena memiliki data sebanyak 3 kali.
6. Berikut ini data hasil panen Pak Sulaiman pada tahun kemarin.

Modus dari data panen tersebut adalah ….
Jawaban:
Modus dari hasil panen tersebut di atas adalah kacang hijau karena paling banyak hasilnya.
Soal matematika kelas 6 semester 2 kurikulum 2013
7. Data nilai ulangan matematika Aqila adalah sebagai berikut :
60, 80, 80, 75, 75, 90, 95, 80, 75, 90
Median data ulangan Ria tersebut adalah …
Untuk mencari median sebuah data, terlebih dulu kita urutkan data tersebut dari yang terkecil. Sehingga menjadi 60, 75, 75, 75, 80, 80, 80, 90, 90, 95.
Setelah itu kita mencari letak dari median tersebut yaitu dengan rumus (jumlah data + 1) : 2
Letak median:
jumlah data + 1 : 2 = (10 + 1) : 2
= 11 : 2 = 5,5
Maksudnya median tersebut terletak di antara urutan no. 5 dan no. 6. Sehingga menjadi sebagai berikut:
no. 5 adalah 80
no. 6 adalah 80
maka: (80 + 80) : 2
= 160 : 2
= 80.
8. Hasil penimbangan berat badan siswa kelas VI Pena Pengajar disajikan dalam diagram batang di bawah ini !

Berapa mean berat badan siswa kelas VI Pena Pengajar tersebut?
Jawaban:
25 x 10 = 250
27 x 15 = 405
30 x 10 = 300
32 x 20 = 640
35 x 15 = 525
Jumlah nilai = 250 + 405 + 300 + 640 + 525
= 655 + 940 + 525
= 1.595 + 525
= 2.120
soal matematika kelas 6 semester 2 pdf
Pencarian terkait:
- soal matematika kelas 6 semester 2 pdf
- soal matematika kelas 6 semester 2 dan kunci jawabannya bangun ruang
- soal uas matematika kelas 6 semester 2 pdf
- soal matematika kelas 6 semester 2 dan kunci jawabannya pdf
- soal matematika kelas 6 dan kunci jawabannya
Demikian yang bisa kami bagikan pada pembahasan kali ini semoga bermanfaat dan menambah wawasan adik adik tentang Soal Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi Terbaru. Terima kasih.




